等腰三角形三线合一及其逆命题的详细解析与应用说明

<股票配资公司>等腰三角形三线合一及其逆命题的详细解析与应用说明

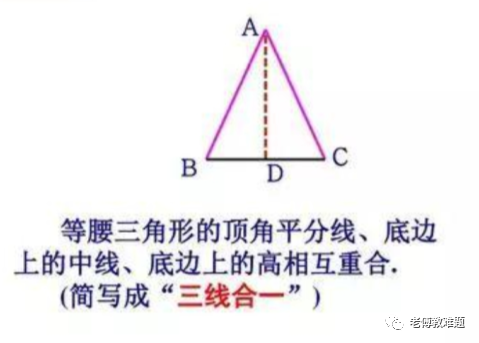
【三线合一】

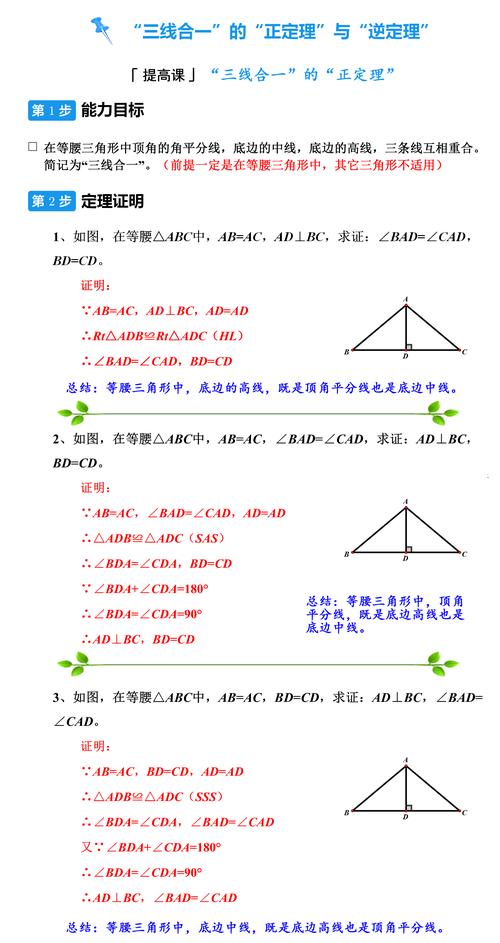
在等腰三角形中顶角的角平分线，底边的中线，底边的高线，三条线段互相重合。简记为”三线合一“ (前提一定是在等腰三角形中，其它三角形不适用)

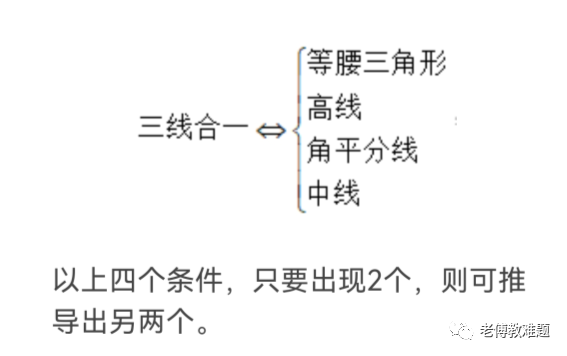
【“三线合一”的逆命题】

在三角形中，高线、中线、角平分线中只要两线重合，则可推出这条线也是第三条线，且这个三角形为等腰三角形。简言之：两线合一，必等腰。

备注：这种逆命题不能作为定理来用，掌握了它和它的证明过程证明三线合一，其目的是为我们解题增加一种重要思路和方法。

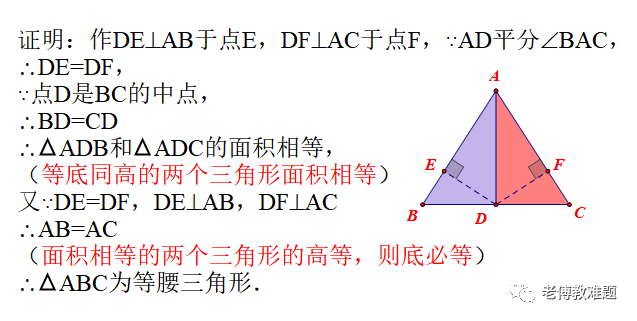
（1）AD平分∠BAC等腰三角形三线合一及其逆命题的详细解析与应用说明，AD⊥BC⇒点D是BC的中点，AB=AC

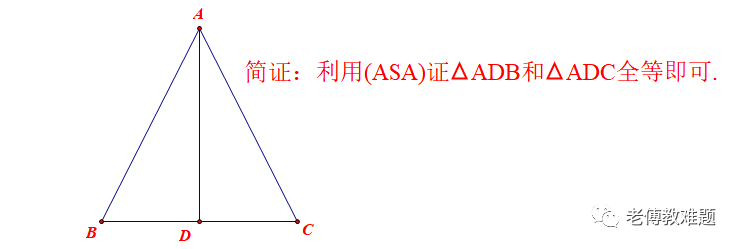
（2）点D是BC的中点，AD⊥BC⇒AD平分∠BAC，AB=AC

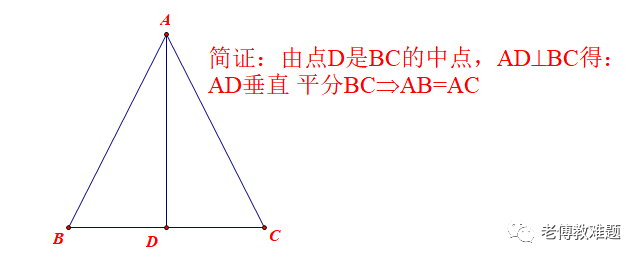
最麻烦是最后一种

（3）点D是BC的中点，AD平分∠BAC，⇒AD⊥BC，AB=AC

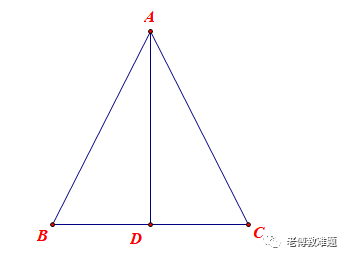
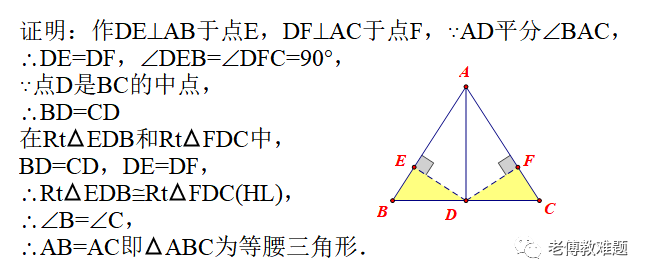
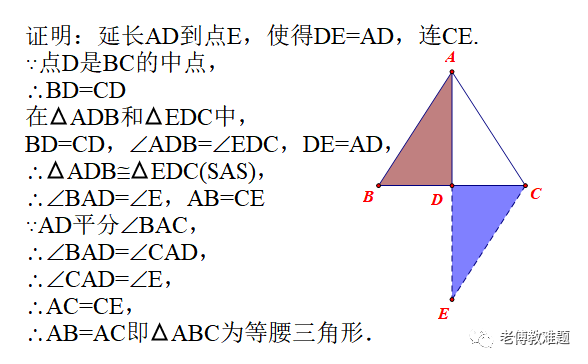
如图，在ABC中，AD平分∠BAC，点D是BC的中点，

求证：ABC是等腰三角形．

下面先看一下一位同学的证明

以上显然是错误的,也就是说少了一个条件.

如果以AD平分∠BAC为切入点，易想到构造轴对称全等（向两边作垂线段，利用角平分线的性质定理）

如果以点D是BC的中点为切入点，易想到倍长构造旋转全等即“8”字型全等（转移线段和角）

如果以点D是BC的中点为切入点，想到等面积，则可用等面积法